Simulating Cloud Motion Vectors From Global Circulation Model Data For Use in OSSEs: A Preliminary, But Useful, Algorithm For Application to Current NASA/NOAA OSSE Projects.
October 18, 2001
Christopher O’Handley
G.D. Emmitt
Steven Greco
Simpson Weather Associates
809 E. Jefferson St.
Charlottesville, VA 22902
1. Introduction
a) Overview
The purpose of this report is to describe the method we have developed for producing realistic cloud motion wind vectors (CMV) for use in OSSEs. Currently, such CMV are obtained by simply using the locations of all observed CMV for the time of interest. The numerical model wind at each location/height is assigned to the CMV at that location, and a gaussian random error is added to each report. This approach has two major shortcomings. First, it may result in CMV in areas where the model has no clouds. Second, there are no correlated errors (such as the slow bias discussed below) in the resulting CMV.
To assure realistic impact assessments using OSSEs, our objective is to produce simulated cloud motion vectors (CMV) that exhibit both random and correlated errors similar to those occurring in practice. We will describe the procedures currently used to produce operational CMV, their spatial distributions, and the magnitudes and sources of errors. We then describe our approach for simulating CMV and their errors using numerical prediction data. We close with a description of future work that is needed to evaluate the resulting winds and further develop the techniques. Note that this paper deals only with CMV from visible and infrared imagery; future work will address the need to simulate CMV from water vapor imagery.
b) Operational cloud motion
wind algorithms
The following description, based primarily on Nieman et al (1997), corresponds most closely to the procedures used to derive GOES CMV at NESDIS.
Generally, a set of 3 infrared (IR) images, at 30 minute intervals, is used to derive CMV. The first step is an image registration analysis between the three images, using the middle image as the starting point. Although the images are navigated and registered prior to receipt by NESDIS, registration errors greater than 2 km (equal to a 1 m/s speed error over 30 minutes) are encountered on a regular basis. The registration correction involves an examination of as many landmarks as possible on the images; the individual shifts are then averaged to produce a single correction in x and y for the image set. Only corrections which exceed 2 km are actually applied, which suggests that the residual registration error is less than 2 km in x and y. However, because of variations in the number of usable landmarks, there are times when the residual error exceeds 2 km. Also, since a single correction is applied across the whole image, there is no way to account for rotational shifts or other nonlinear types of error.
The second step is target identification. A grid of approximately 60x60 km is used to search the first image of a triplet for sufficiently non-homogeneous cloud patterns. The algorithm uses spatial-coherence analysis to identify the highest (brightest) cloud in the scene, and find the region of strongest brightness gradient. The cloud is identified as a target if the gradient exceeds a certain magnitude. While any type of cloud can be tracked, scenes with multiple cloud decks are eliminated because these make cloud height difficult to determine.
Once a target has been identified, the cloud top height is determined. Several methods are available. The simplest, which is used as a back-up, is the infrared window approach, in which the coldest 20% of the sample is assumed to represent the cloud top temperature, and height is determined by comparison with a temperature profile from a numerical forecast. More advanced techniques, such as the CO2 slicing and H2O intercept methods (Nieman et al, 1993), are used when possible, and are particularly beneficial in cases where the target cloud is semi-transparent (and thus susceptible to contamination by surface radiation). Both methods use information from multiple channels and require both cloudy and clear-sky radiances. Though more accurate, these techniques also rely on information from numerical forecasts to estimate radiances. The current GOES satellites have sensors which allow use of the H2O intercept, whereas 1993-era GOES sensors required use of CO2 intercept. Recently, techniques have also been developed that enable estimation of cloud base heights for low-level (below 700 mb) cloud tracers, as it is known that such clouds generally move with the wind speed close to cloud base.
The
fourth step is the actual tracking of target clouds from image to image. The
position of the target on image 2 is estimated using the wind predicted by a
numerical forecast model. A correlation procedure is then used to search the
second image; if the maximum correlation exceeds a pre-defined threshold, the
target is identified and the resulting 30 minute shift defines the first CMV.
This step is repeated using images 2 and 3, which yields a second CMV. If the difference between the two vectors is
sufficiently small (generally about 5 m/s), an average CMV is computed from the
two vectors, and the resulting vector is passed on to the quality control
system.
While
the above steps are fairly similar among the various CMV producers
(Butterworth, 1997a), the quality control procedure which follows differs
considerably (Holmlund et al, 2001). The most advanced, completely automated
procedures are implemented at EUMETSAT and NESDIS. The NESDIS technique, known
as the auto-editor, involves two steps of a fully three-dimensional recursive
filter objective analysis. In the first step, a background analysis is produced
using a numerical forecast along with all available non-CMV observations. This
is followed by a second step which incorporates the CMV. During this process, a
penalty function is used to re-assign the heights of the CMV to the level of
best fit if necessary (the adjustment is limited to 150 mb), and winds which
differ greatly from the resulting analysis are flagged. At EUMETSAT, the
individual CMV vectors are put through a series of consistency tests that
primarily compare them to other CMV reports, though one test involves a model
forecast field. Both methods also yield quality control flags for each CMV.
c) Known errors in CMV
Recent
comparison studies between CMV and co-located radiosondes indicate that rms
error values of CMV increase with height, ranging from about 3-4 m/s below 700
mb, to 4-6 m/s between 400 and 700 mb, and 6-8 m/s at higher levels (Tomassini
et al, 1999). It should be noted that these are not absolute accuracies, as
radiosondes themselves have errors ranging from roughly 2 m/s (low levels) to 4
m/s (high levels). More troubling is a persistent slow bias in CMV,
particularly at higher wind speeds. Some studies have found the slow bias to be
as large as 5-6 m/s in uncorrected CMV. This error is so important (jetstream
wind speeds are already underforecasted by numerical models) that NESDIS
actually implements a “slow bias correction” as part of their auto-editor. All
CMV whose speed exceeds 10 m/s are augmented with 7% of the forecast wind speed
at that location. The corrected CMV that result from the auto-edit procedure
still exhibit a slow bias of approximately 1-2 m/s, depending on windspeed.
While
the magnitudes of CMV errors have been well defined, the exact causes of the
errors are somewhat uncertain. It has been suggested that the slow bias may be
due to non-representative cloud motions, i.e. that the tracer clouds, generally
cirrus, do not move with the winds near jet level. This has not been
conclusively shown, although it is well known that other clouds do not move
with the wind at cloud top (the height at which the CMV is assigned). For
instance, tropical cumulus have been shown to move with the wind near cloud
base, and there is often a 1-2 m/s difference between the winds at cloud base
and cloud top (Peslen et al, 1986). It would seem that other explanations could
account for the slow bias. In particular, the presence of sub-visual cirrus
clouds above the target clouds could contaminate the height assignment, making
the target cloud appear higher. Where the
windspeed increases upward, the effect would be to place a slower CMV
higher up in the atmosphere, in a region with faster windspeed – thus
introducing a slow bias. This will be examined in more detail below.
More
generally, the height assignment process is susceptible to numerous errors. In
the case of semi-transparent cloud targets, contamination by upwelling surface
radiation can corrupt the height assignment. The CO2 and H2O
techniques help circumvent this problem, but at the expense of introducing
information from numerical forecast models. In certain situations, this
presumably could lead to large errors in height assignment. Other sources of
error include image registration shifts, inaccuracies in the correlation
algorithms used to identify and track cloud tracers, and cloud development and
dissipation.
d) CMV data coverage
At
present, CMV are produced from the following 5 satellites: GOES-W (135 W),
GOES-E (75 W), METEOSAT (0 W), GMS (140 E), and INSAT (80 E). Generally, winds
are produced within about 45-60° from the satellite
sub-point. This results in nearly global coverage within about 45° of the equator. However, the exact types of
winds (infrared/visible/water vapor), as well as the techniques and quality
control procedures, differ among the producers. For comparison, in 1993 there
were 4 satellites producing CMV (the above minus INSAT), which resulted in a
gap of 30-45° in longitude in the Indian
Ocean region.
e) CMV use in data
assimilation
Because
of the differences in types of winds produced, methods used, and resulting
accuracies, the major weather prediction centers have put in place severe
restrictions on the use of CMV in their data assimilation systems. For example,
at ECMWF (Butterworth 1997b), winds from INSAT are not used, nor are any
visible winds above 700 mb. Also rejected are IR winds over land that are north
of 20° N, and IR winds over land below 500 mb that
are south of 20° N. Furthermore, all high-density winds are
thinned to one observation per (approximately) 1.25° box at each model level; the observations
are chosen on the basis of the quality control flags. Note that other types of
restrictions are applied to water vapor and sounder winds, which are not
discussed here. At NCEP, INSAT winds are not used, GMS winds are used
everywhere, and GOES and Meteosat winds are used everywhere south of 20° N, and only over the ocean elsewhere. Note
that CMV use in data assimilation is constantly being evaluated and modified,
so this description may not be 100% accurate.
2. Data
For this study, simulated cloud track winds were produced using data from an ECMWF T213 spectral model 30-day forecast, which serves as a “nature run” for the NPOESS OSSE project. The data was available on a one half degree latitude/longitude grid at 31 pressure levels from 1000 to 100 mb, every 6 hours, from 06 UTC 2/5/1993 to 00 UTC 3/6/1993. Parameters that were used include cloud fraction, cloud liquid water content, temperature, and u and v wind components. Low-level cloud fractions (below 800 mb) were corrected to eliminate the global under-estimation of low cloud in the nature run (Masutani et al, 1999).
3. Methods and Results
a) Cloud-motion winds:
target selection
At
each model grid point within 60° of a satellite sub-point, a
“satellite cloud view” (SCV) is calculated by applying cloud overlap
assumptions to the model cloud fractions. For contiguous cloud layers (those in
successive model layers), maximum overlap is assumed, i.e. the cloud layers are
considered vertically stacked. As an example, assume that the model cloud
fraction is 40% in the higher of 2 layers, and 50% in the next layer. The SCV
of the first layer is 40%. Applying maximum overlap, 40% of the cloud in the
second layer is considered obscured, leaving an additional SCV of 10% in that
layer. If the second layer has less cloud than the higher layer, none of it can
be seen. For non-contiguous cloud layers, i.e. cloudy layers separated by at
least one clear layer, random overlap is applied. Using the above example, the SCV in the lower layer could range
from 10% to 50%. If the higher layer has 40% and the lower layer 30%, then the
SCV in the lower layer could range from 0-30%, i.e. all of the cloud might be
seen. The random overlap essentially states that non-contiguous cloud layers
are considered to be completely unrelated dynamically.
The
SCV profile is then examined from the top down to determine if a suitable cloud
tracer exists. Any layer with a SCV cloud fraction of between 0.05 and 0.25 is
assumed to be a potential tracer, and the first such level encountered is
chosen as the tracer for that location. It is assumed that if the SCV is less
than 0.05, there is insufficient cloud for tracking. On the other hand, if SCV
exceeds 0.25, the cloud is assumed to be more stratiform in nature, with
insufficient edges or brightness variations for tracking to be successful. This approach is based on the general
targeting algorithms described earlier, which rely on inhomogeneities in the
cloud field. The exact SCV range is somewhat arbitrary, and has been adjusted
to give “reasonable” distributions of CMV. Further work is needed to evaluate
the CMV distributions that result. In particular, these values have been
adjusted to give CMV totals that are close to 1993 levels; current operational
CMV totals are much higher.
Once
the target has been located, the T213 model u and v wind components are
recorded as the true wind associated with the CMV at that location. An example
of the distribution of CMV produced using this method is shown in Figure 1.
Panels a and b contain the column totals of opaque and cirrus cloud (SCV),
which show the distribution of clouds and weather systems. Panels c-f show the
locations of the CMV in 4 different layers, and Table I lists the number of CMV
for this case, statified by height and cloud fraction. The total number of CMV
is about 4 times larger than the number of true CMV for the same time period,
and the vertical distribution is too heavily skewed to the low layers. It is assumed that inclusion of cirrus
targets would increase the number of high level CMV while reducing those at
lower levels; this remains for future work. However, the spatial distribution
of the simulated CMV is reasonably similar to observed distributions of CMV in
1993, especially if the simulated vectors are randomly thinned to the same
total number. This is demonstrated in Figure 2 (note that these figures are 12
hours apart).
b) Modeling of Slow Bias
As
indicated earlier, comparative studies between CMV and radiosonde winds have
revealed the presence of a slow bias which increases with wind speed. It has
been suggested that these types of errors exhibit spatial correlations which
could have a strong negative impact on numerical weather prediction
(Butterworth, 1997b; Holmlund et al, 2001). Unfortunately, no studies have
clearly documented such a spatial correlation, though it seems reasonable to
suspect that the bias patterns might be correlated along the path of jet
streams.
The
cause of the slow bias is not known. However, it has been attributed to non-representative cloud motions near the
jet stream or, in the specific case of water vapor winds, to improper height
assignment or edge effects on cloud tracking (Daniels et al, 2000). Our attempt
to simulate a slow bias is based on the idea that a slow bias may be the result
of contamination of the cloud height estimate by thin or sub-visual cirrus
clouds. If present, such clouds would make the target cloud appear to be colder
than it really is, and thus higher in the atmosphere. Since winds generally
increase upward throughout most of the troposphere, this would effectively
introduce a slow bias by making a lower, slower-moving cloud appear to be at a
higher height, where windspeeds are faster.
Our
approach is as follows. For each profile where a cloud target is found, we
determine if thin cirrus cloud is likely to be present above the target cloud.
If such cirrus is predicted, then the pressure difference dp between the highest cirrus
and the target cloud is calculated. dp
is multiplied by a gaussian random deviate (between 0-1), and the resulting
value dpadj is used to adjust the pressure of the target cloud upward to a new
apparent pressure (papp).
The model wind speed at this new level is the equivalent of the true, or
radiosonde speed. However, the wind speed at the original level is still
applied to the CMV. This introduces a “cold bias” error which may or may not
also be a negative wind speed error, depending on the vertical profile of wind
speed.
As
it turns out, this procedure does produce a slow bias. Table II shows the
resulting bias values for all CMV above 700 mb, for the case shown in Figure 1.
The speed bias is tabulated two ways, with respect to the true or radiosonde
speed (BIAS1) and then with respect to the CMV speed (BIAS2). BIAS1, which is
equivalent to the way the values are usually reported in the literature, shows
a strong slow bias that increases dramatically with increasing wind speed. The
bias values for speeds above 30 m/s greatly exceed any published statistics,
which may indicate that we are allowing vertical adjustments that are too
large. However, it should be noted that the sample size is relatively small.
BIAS2 shows a much more constant slow bias across all speed ranges. This
differs from the recent findings of Lalaurette and Garcia-Mendez (2000), who
plotted the slow bias for winds above 400 mb versus CMV speed. They found a
linear increase in the slow bias from 0 m/s at 15 m/s to –5 m/s at 45 m/s.
Unfortunately, we have not seen other observational studies in which the slow
bias is tabulated based on CMV speed for comparison. Our overall simulated slow
bias of –2.15 m/s is reasonably close to recently published values (Tomassini
et al, 1999)
The
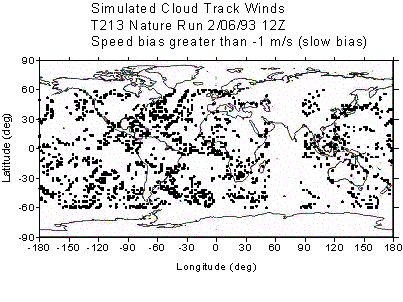
other issue regarding the slow bias is horizontal correlation of the errors.
Figure 3 shows those CMV that have a slow bias greater than –1 m/s (panel a)
and those that have a fast bias greater than +1 m/s (panel b). Clearly this
procedure does introduce concentrated areas of slow bias, in regions where
cirrus clouds are found (compare to Figure 1). Unfortunately, there are no
published studies showing spatial distributions of bias errors in operational
CMV for comparison. However, observational studies have shown that the slow
bias is predominantly a mid-latitude phenomenon, and this is reflected in the
spatial distributions shown in Figure 3.
c) Image Registration Errors
As
noted earlier, NESDIS applies a registration correction to each image triplet
if the calculated registration errors exceed 2 km. However, the accuracy of the
correction depends on the number and distribution of landmarks, which can vary
considerably. Thus, errors exceeding 2 km may be fairly common. In addition,
rotational and non-linear errors cannot be eliminated using the current
approach. Since a 2 km shift in 30 minutes introduces a wind speed error of 1.1
m/s at nadir (and more near the edge of the image), this is obviously a
significant source of correlated error that must be included in simulated CMV.
The
main difficulty in simulating these errors is the spherical nature of the
earth. A simple west-east registration shift will introduce only zonal wind
errors, though the magnitude of the error will increase toward the edges of the
image. However, a north-south shift will introduce both longitudinal and zonal
wind components, with the ratio of the components changing depending on latitude
and longitude. To quantify the distribution and magnitude of wind errors across
the CMV domain, map projection equations are used. We have used the equations
for the equatorial azimuthal orthographic projection:
x
= cos(lat)sin(lon) (1)
y = sin(lat)
(2)
The resulting projection, shown in Figure 4, is not exactly the satellite projection, but it is very close.
The procedure to estimate wind errors introduced by a registration shift is as follows. First, an x,y shift (dx, dy) is randomly assigned for the image as a whole. This value is assumed to be valid at nadir. Then, at the location of each cloud target, the following is done. First, equations (1) and (2) are used to calculate the unshifted x and y positions of the point based on the true latitude and longitude; this location is recorded as xtrue and ytrue. Next, the shifted longitude position xshift is determined from xtrue + dx, and a new longitude is back-calculated from equations (1) and (2). This is repeated for latitude, resulting in a new (or apparent) latitude and longitude for the location. Finally, the differences between the true and apparent latitudes and longitudes are used to determine the distance shifts in km, which yields a wind speed which corresponds to the image registration error.
Figure 5 shows the estimated wind errors resulting from registration shifts of 2 km over 30 minutes. A due eastward shift (panel a) causes westerly winds across the domain, with speeds of 1-2 m/s. The wind speed is constant in latitude, but increases toward the western and eastern edges of the domain. A northward shift (panel b) causes a symmetric pattern, with southerly winds predominating near the center and increasing zonal components toward the corners. Total wind speeds can exceed 3 m/s at the corners of the map. A combined northward/eastward shift (panel c) causes a more complicated pattern, with wind speeds greater than 2 m/s over significant parts of the domain and maxima exceeding 5 m/s in the SW and NE corners
4.
Discussion/Future Work
We have produced simulated CMV whose spatial distribution appears broadly similar to operational CMV from 1993. However, the vertical distribution is too highly skewed to lower altitudes, and the total number of vectors is too large by a factor of 4. Several items need to be explored to fix these problems. First, we need to examine the cloud overlap calculation, particularly the method used to identify thin (sub-visual) cirrus clouds. After this, we will need to add cirrus targets into the tracking algorithm. Operational CMV producers do track cirrus clouds, and these make up a significant source of CMV. It is presumed that using cirrus targets would give us a more realistic vertical distribution of CMV; it might also change the slow bias results significantly. We will need to modify the algorithm to simulate CMV of the density that are currently produced, which greatly exceeds the levels of 1993. This will involve testing different cloud fraction ranges for the target cut-off, and examining the spatial patterns of CMV that result.
We need to more carefully analyze the results of our slow bias simulation. Observational studies frequently present the bias statistics as a function of latitude and height; we have only looked at the entire sample above 700 mb. We will also look at the spatial patterns to determine how error magnitudes are correlated; this should also involve an examination of the direction errors (observations suggest that there is little directional component to the slow bias). This process should help us determine if we are producing a slow bias for the wrong reason.
Many researchers have indicated that CMV are frequently contaminated by surface radiation, which would tend to produce a warm, or low, bias in the cloud heights. Seemingly, this would tend to produce a fast bias and in fact at slower wind speeds, observed CMV do tend to show a slightly positive bias (Lalaurette and Garcis-Mendez, 2000). We need to incorporate a surface radiation component to our height adjustment, probably only in cases where the target cloud is “thin”. Potentially, a single, thin target cloud could be affected by both a surface-induced warm bias and a cirrus-induced cold bias, of varying magnitudes. It will be interesting to see how these effects combine, and whether a slow bias is still present in our simulated CMV.
Finally, our registration error simulator could be improved by incorporating the map projection equations for the true satellite projection. It is believed that this would lead to slightly larger induced winds, especially near the edges of the domain. We may also want to add the ability to create rotational image shifts, though this may not be necessary as the current approach serves the purpose of introducing wind errors that are correlated across the satellite domain.
5) References
Butterworth,
P., 1997a: NWP on-line scientific note no, 2: Investigation into satellite
winds – I. Production.
Butterworth,
P., 1997b: NWP on-line scientific note no. 3: Investigation into satellite
winds – II. Treatment at UKMO.
Daniels,
J., C. Velden, W. Bresky and A. Irving, 2000: Status and development of
operational GOES wind products. Proc. Fifth Intl. Winds Workshop, Lorne,
Australia.
Holmlund,
K., C.S. Velden, and M. Rohn, 2001: Enhanced automated quality control applied
to high-density satellite-derived winds. Mon.
Wea. Rev., 129, 517-529.
Lalaurette,
F. and A. Garcia-Mendez, 2000: Monitoring satellite winds at ECMWF. Proc. Fifth Intl. Winds Workshop, Lorne,
Australia
Masutani,
M, K.A. Campana and S-K Yang, 1999: Note on cloud cover of the ECMWF nature run
used for OSSE/NPOESS project. Office note 427. NCEP.
Nieman,
S.J., J. Schmetz and W.P Menzel, 1993: A comparison of several techniques to
assign heights to cloud tracers. J. Appl.
Met., 32, 1559-1568.
Nieman,
S.J., W.P. Menzel, C.M. Hayden, D. Gray, S.T. Wanzog, C.S. Velden, and J.
Daniels, 1997: Fully automated cloud-drift winds in NESDIS operations. Bull. Amer. Met. Soc., 78, 1121-1133.
Peslen,
C.A., S.E. Koch and L.W. Uccellini, 1986: The effect of the arbitraty level
assignment of satellite cloud motion wind vectors on wind analyses in the
pre-thunderstorm environment. J. Clim.
Appl. Met., 25, 615-632.
Tomassini,
M., G. Kelly and R. Saunders, 1999: Use and impact of satellite atmospheric
winds on ECMWF analyses and forecasts. Mon.
Wea. Rev., 127, 971-986.
Table I: Number of cloud track winds for each atmospheric layer, and range of cloud fraction for those winds.
|
|
CLOUD FRACTION |
|
||
|
LEVEL |
0-10% |
10-20% |
20-30% |
TOTAL |
|
high
|
29 |
67 |
52 |
148 |
|
middle |
359 |
633 |
255 |
1247 |
|
low |
1136 |
1319 |
369 |
2824 |
|
pbl |
685 |
460 |
107 |
1252 |
|
|
2209 |
2479 |
783 |
5471 |
Table
II: Speed bias (m/s) for all simulated CMW above 700 mb. BIAS1 is the bias as
tabulated by radiosonde (true) speed, with NUM1 the number of observations for
that category. BIAS2 and NUM2 are the same, but tabulated against the CMW
speed.
Speed range |
BIAS1 |
NUM1 |
BIAS2 |
NUM2 |
|
0-10 m/s |
0.29 |
1215 |
-2.41 |
1571 |
|
10-20 m/s |
-2.95 |
1126 |
-1.77 |
992 |
|
20-30 m/s |
-5.23 |
378 |
-2.43 |
241 |
|
30-40 m/s |
-8.65 |
127 |
-2.29 |
58 |
|
40-50 m/s |
-10.59 |
21 |
-1.48 |
5 |
|
|
-2.19 |
2867 |
|
|
|
|
|
|
|
|
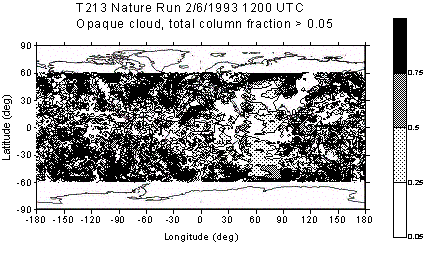
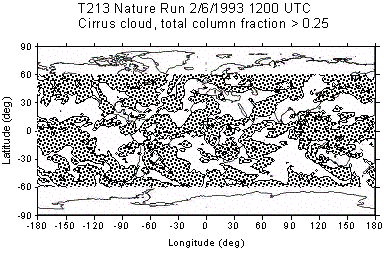
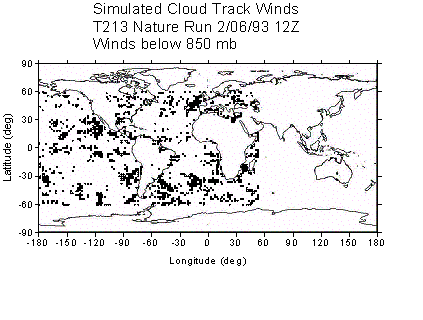
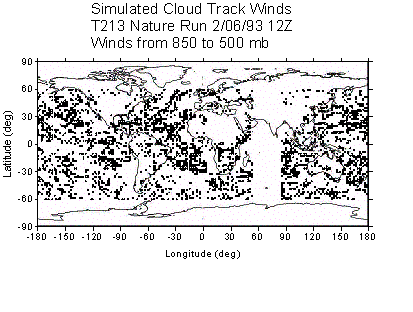
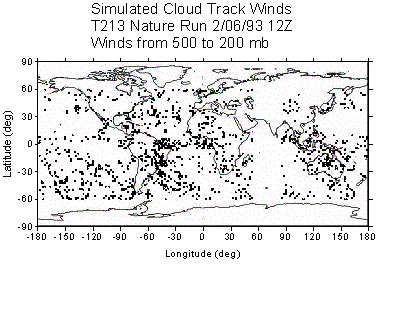
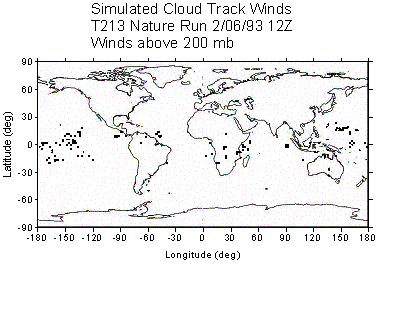
Figure 1: Simulated cloud track winds for 1200 UTC 2/6/1993. (a) Column total cirrus (b) column total opaque cloud (c) Low-level CMV (below 850 mb)
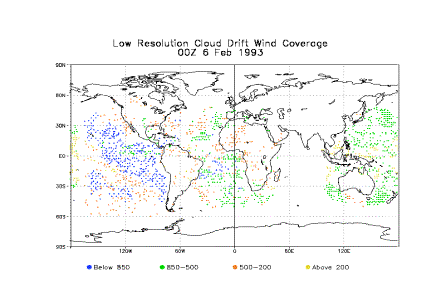
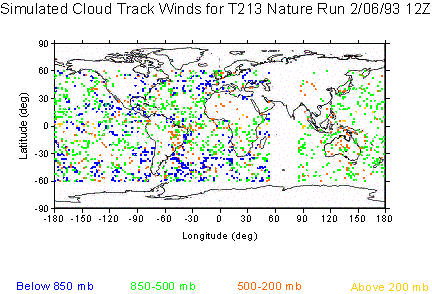
Figure 2: Comparison between actual cloud track winds from 1993 and simulated winds. (a) Actual CMV from 0000 UTC February 6, 1993 (b) simulated CMV from Figure 1, randomly thinned to approximately the same density as the observed winds.
.
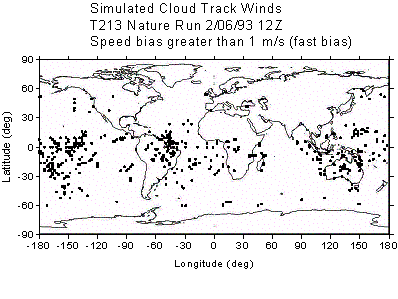
Figure 3: Locations of CMV above 700 mb that exhibit a bias
greater than 1 m/s. (a) slow bias (b) fast bias
Figure 4: Map projection used to simulate registration errors. Latitude and longitude shown at 10° intervals.

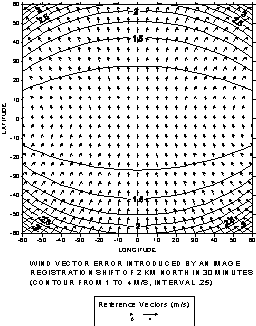
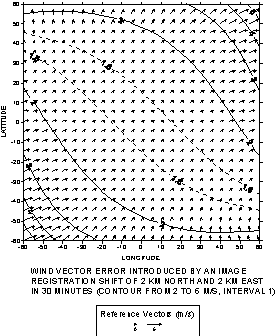
Figure 5: Wind vectors resulting from image registration shifts of 2 km in 30 minutes. (a) eastward shift (b) northward shift (c) northward and eastward shift.